

This method also applies the same logic but we use a direct formula to find the area of a rectangle. Now, we know that the length = 4 cm, width = 3 cm. In this case, the width can be calculated using the formula, width = ⎷Īfter substituting the given values, we get, width = ⎷ The width of the rectangle is missing and it can be calculated using the Pythagoras theorem because the diagonals of a rectangle form 2 right-angled triangles. Let us understand this using an example.Įxample: Find the area of a rectangle whose length is 4 cm and whose diagonal is 5 cm. We can find the value of the missing side using the Pythagoras theorem and then find the area. There can be two ways in which we can find the area of a rectangle using the diagonal.
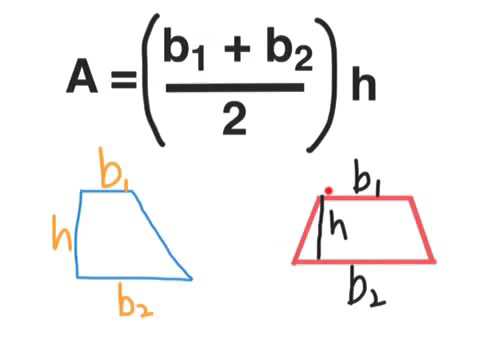
There are two diagonals in a rectangle and both are of equal length. The diagonal of a rectangle is the straight line inside the rectangle connecting its opposite vertices. The area of a rectangle can be calculated if the diagonal and one side is given. Similarly, if the length and width of any rectangle is given in cm, then the area will be expressed in square centimeters (cm 2). In this case, since the length and width of this rectangle is given in 'inches', the area is measured and written in square inches (in 2). In other words, 12 unit squares can fit in the given rectangle covering all its space and this is termed as the area of a rectangle. So, a rectangle whose sides are 4 inches and 3 inches has an area of 12 square inches or 12 in 2. Since 12 equal-sized squares can fit in this rectangle, they also show the space occupied by the whole rectangle. Observe the figure given below in which we can divide the figure into 12 small squares, each of which is a square, that is, 1 inch on each side, that is, 1 square inch. Now, let us understand the reason for which the area of a rectangle is expressed in square units using the following example.Įxample: The length of a rectangle is 4 inches and its width is 3 inches. We know that length is always measured and expressed in units like cm, inches, etc. The unit of the area of a rectangle is expressed in square units. Therefore, the area of the rectangle = 60 square units. Therefore, area of the rectangle = 15 × 4 = 60 Substitute 15 for 'l' and 4 for 'w' in this formula.

The formula to find the area of a rectangle is A = l × w. Solution: Given, length = 15 units and width = 4 units. Let us take an example to understand the calculation of the area of a rectangle.Įxample: Find the area of the rectangle whose length is 15 units and width is 4 units. Step 3: Give the answer in square units.Step 2: Find the product of the length and width values.Step 1: Note the dimensions of length and width (breadth) from the given data.The area of a rectangle can be calculated using the steps given below: Where a, b, c, and d are the four sides of the trapezoid.The area of a rectangle is the product of its length and width (breadth). The perimeter of a trapezoid is the sum of all four sides. Where b1 and b2 are the bases, and h is the height of the trapezoid. The area of the trapezoid is calculated by the formula: The non-parallel sides of the trapezoid are known as the legs, and the parallel sides are known as the bases. Where a, b, c, and d are the four sides of the parallelogram.Ī trapezoid is a quadrilateral with one pair of parallel sides. The perimeter of a parallelogram is the sum of its all four sides. Where b is the base length, and h is the height. To find the area of a parallelogram, we have the formula:Ī = b x h.

In a parallelogram, the two opposite sides and the angles are congruent, while the consecutive angles are supplementary. Where l is the length of the sides, and w is the width of the triangle.Ī parallelogram is a quadrilateral that has two parallel opposite sides. Area of the triangle is half the area of the rectangle. Where a, b, and c are the three sides of a triangle.Īrea of the triangle is the space occupied by the shape. Area is measured in square unitsĪrea and Perimeter of the Triangle - For a triangle, we can find the perimeter by adding the lengths of its three sides. The area is the measurement of the area enclosed by the plane region. The perimeter of a shape is the length of its boundary, usually measured in the same units as that of length.
Find area of rectangle trapezoid how to#
How to Find Area and Perimeter of Triangle, Parallelogram, and Trapezoid? Area and Perimeter of Triangles, Parallelograms, and Trapezoids Worksheets


 0 kommentar(er)
0 kommentar(er)
